Mobile Inverted Pendulum

Simple Planar Model

Fig1. - Planar MIP Picture (left) and Schematics (right).

code

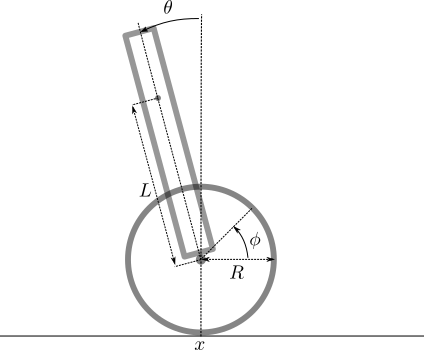
The derivation of a space state equation is adapted from \cite{ostovari2014}

Notations

• $m_w$, $m_b$, $I_w$, $I_b$: respectively wheel and body masses and inertias
• $L$: distance between wheel axis and body center of mass
• $R$: wheel radius
• $\theta$: angle between vertical and body axis
• $\phi$: angle between horizontal and the wheel
• $x$: horizontal coordinate of the wheel axis

Kinematics

Position of the body center of mass: $\begin{equation} \vect{r} = \begin{pmatrix}x-L\sin{\theta} \\ R+L\cos{\theta}\end{pmatrix} \end{equation}$

Velocity of the body center of mass: $\begin{equation} \dot{\vect{r}} = \begin{pmatrix}\dot{x}-L\dot{\theta}\cos{\theta} \\ -L\dot{\theta}\sin{\theta}\end{pmatrix} \end{equation}$

Acceleration of the body center of mass: $\begin{equation} \ddot{\vect{r}} = \begin{pmatrix} \ddot{x}-L\ddot{\theta}\cos{\theta} + L \dot{\theta}^2\sin{\theta}\\ -L\ddot{\theta}\sin{\theta} - L \dot{\theta}^2 \cos{\theta} \end{pmatrix} \end{equation}$

The \emph{no slip} hypothesis also brings: $\begin{equation} x = -R \phi \end{equation}$

Dynamics

• Angular acceleration of the wheel $\begin{equation} I_w \ddot{\phi} = \tau - F R \end{equation}$

• Linear acceleration of the wheel $\begin{equation} m_w \begin{pmatrix} \ddot{x} \\ 0 \end{pmatrix} = \begin{pmatrix}-P_x - F \\ N - P_y -m_w g \end{pmatrix} \end{equation}$

• Angular acceleration of the body $\begin{equation} I_b \ddot{\theta} = -\tau + P_y L \sin{\theta} + P_x L \cos{\theta} \end{equation}$

• Linear acceleration of the body in $\vect{i}$ direction: $\begin{equation} m_b (\ddot{x} -\dot{\theta}L\cos{\theta} + \dot{theta}^2 L \sin{\theta}) = P_x \end{equation}$

State Space Equation

$$\begin{equation} (m_bRL\cos{\theta}) \ddot{\phi} + (I_b + m_bL^2) \ddot{\theta} = m_b g L \sin{\theta} - \tau \end{equation}$$

\begin{equation} \left(I_w + (m_b+m_w)R^2\right) \ddot{\phi} + (m_b R L \cos{\theta}) \ddot{\theta} = m_b R L \dot{\theta}^2 \sin{\theta} + \tau \end{equation}

or matricially

$$\begin{equation} \begin{pmatrix}a & b \\ c & a \end{pmatrix} \begin{pmatrix}\ddot{\phi} \\ \ddot{\theta} \end{pmatrix} = \begin{pmatrix} d \\ e \end{pmatrix} \end{equation}$$

with

$$\begin{equation} a = m_bRL\cos{\theta} \quad b = I_b + m_bL^2 \quad c = I_w + (m_b+m_w)R^2 \end{equation}$$

and

$$\begin{equation} d = m_b g L \sin{\theta} - \tau \quad e = m_b R L \dot{\theta}^2 \sin{\theta} + \tau \end{equation}$$

When the system has full rank ($a^2-bc \ne 0$), equations can be separated, leading to

$$\begin{equation} \begin{pmatrix}\ddot{\phi} \\ \ddot{\theta} \end{pmatrix} = \frac{1}{a^2-bc}\begin{pmatrix}a & -b \\ -c & a \end{pmatrix}\begin{pmatrix} d \\ e \end{pmatrix} \end{equation}$$

or

$$\begin{equation} \begin{pmatrix}\ddot{\phi} \\ \ddot{\theta} \end{pmatrix} = \frac{1}{a^2-bc}\begin{pmatrix} ad-be \\ -cd+ae\end{pmatrix} \end{equation}$$

which expands to:

$$\begin{equation} \begin{cases} \ddot{\phi} = \\ \ddot{\theta} = \end{cases} \end{equation}$$

References

\bibitem{ostovari2014} Saam Ostovari et al {\em The dynamics of a Mobile Inverted Pendulum (MIP)} 2014.