Planar VTOL with Pole

The PVTOL with Pole is a planar simplification of the problem of balancing a pole on top of a quadrotor, as demonstrated by Raffaello d’Andrea in his 2013 TED talk.

Fig1. - Raffaello d'Andrea TED conference.

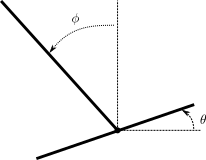
The following figure describes the variables and parameters of the model:

Fig2. - PVTOL with pole notations.

We will start by deriving a dynamic model for the PVTOL with pole system.

It can be seen that the vector $q=\begin{pmatrix}x&z&\theta&\phi\end{pmatrix}^T$ can be used a generalized coordinates as it uniquely describes the configuration of the system.

Kinematic

Assumingt that the pole is constrained to pivot at the center of the PVTOL, the position of the center of mass of the pole is then given by:

$$\begin{cases} x_p = x - l \sin{\phi} \\ z_p = z + l \cos{\phi} \end{cases}$$

Computing the time derivative of the above equation, we get the velocity of the pole’s center of mass as:

$$\begin{cases} \dot{x}_p = \dot{x} - l \dot{\phi} \cos{\phi} \\ \dot{z}_p = \dot{z} - l \dot{\phi} \sin{\phi} \end{cases}$$

Noting $v^2=\dot{x}^2+\dot{z}^2$ and $v_p^2=\dot{x}_p^2+\dot{z}_p^2$, the relationship between the pvtol and pole centers of mass velocities is expressed as:

$$v_p^2 = \dot{x}^2 + \dot{z}^2 + l^2\dot{\phi}^2 -2l\dot{\phi}\left( \dot{x}\cos{\phi}+\dot{z}\sin{\phi}\right)$$ $$v_p^2 = v^2 + l^2\dot{\phi}^2 -2l\dot{\phi}\left( \dot{x}\cos{\phi}+\dot{z}\sin{\phi}\right)$$

Energy

	Kinetic Energy	Potential Energy
pvtol	$$ T_v = \frac{1}{2} Mv^2 + \frac{1}{2} J \dot{\theta}^2$$	$$ V_v = Mgz$$
pole	$$ T_p = \frac{1}{2} mv_p^2 + \frac{1}{2} j \dot{\phi}^2$$	$$ V_p = mgz_p$$

Lagrangian

$$\mathscr{L} = T - V$$ $$\mathscr{L} = \frac{1}{2}Mv^2 + \frac{1}{2} J \dot{\theta}^2 +\frac{1}{2}mv_p^2 + \frac{1}{2} j \dot{\phi}^2 - Mgz - mgz_p$$

Expanding with state variables, we get:

$$\begin{multline} \mathscr{L} = \frac{1}{2} \left( M+m \right) \left( \dot{x}^2 + \dot{z}^2 \right) + \frac{1}{2} J \dot{\theta}^2 + \frac{1}{2} j \dot{\phi}^2 \\ + \frac{1}{2}m\left( l^2\dot{\phi}^2 -2l\dot{\phi}\left( \dot{x}\cos{\phi}+\dot{z}\sin{\phi}\right) \right) - \left( M+m \right) g z - mgl \cos{\phi} \end{multline}$$

Partial derivatives of the Lagrangian with respect to the state vector components are:

$$\begin{cases} \frac{\partial{\mathscr{L}}}{\partial{x}} = 0 \\ \frac{\partial{\mathscr{L}}}{\partial{z}} = - \left( M+m \right) g\\ \frac{\partial{\mathscr{L}}}{\partial{\theta}} = 0 \\ \frac{\partial{\mathscr{L}}}{\partial{\phi}} = ml \left( \dot{\phi} \left( \dot{x}\sin{\phi} - \dot{z}\cos{\phi}\right) + g \sin{\phi}\right)\\ \frac{\partial{\mathscr{L}}}{\partial{\dot{x}}} = \left( M+m \right) \dot{x} - ml\dot{\phi}\cos{\phi}\\ \frac{\partial{\mathscr{L}}}{\partial{\dot{z}}} = \left( M+m \right) \dot{z} - ml\dot{\phi}\sin{\phi}\\ \frac{\partial{\mathscr{L}}}{\partial{\dot{\theta}}} = J \dot{\theta}\\ \frac{\partial{\mathscr{L}}}{\partial{\dot{\phi}}} = j \dot{\phi} + ml \left( l\dot{\phi} - \left( \dot{x}\cos{\phi}+\dot{z}\sin{\phi} \right)\right)\\ \end{cases}$$

Lagrange Equations

*

$$\frac{d}{dt}\left( \frac{\partial{\mathscr{L}}}{\partial{\dot{x}}} \right) - \frac{\partial{\mathscr{L}}}{\partial{x}} = F_x$$ $$\left( M+m \right) \ddot{x} - ml \left( \ddot{\phi} \cos{\phi} - \dot{\phi}^2\sin{\phi}\right) = -(f_1+f_2) \sin{\theta}$$

*

$$\frac{d}{dt}\left( \frac{\partial{\mathscr{L}}}{\partial{\dot{z}}} \right) - \frac{\partial{\mathscr{L}}}{\partial{z}} = F_z$$ $$\left( M+m \right) \ddot{z} - ml \left( \ddot{\phi} \sin{\phi} + \dot{\phi}^2\cos{\phi}\right) + \left( M+m \right) g = (f_1+f_2) \cos{\theta}$$

*

$$\frac{d}{dt}\left( \frac{\partial{\mathscr{L}}}{\partial{\dot{\theta}}} \right) - \frac{\partial{\mathscr{L}}}{\partial{\theta}} = M_{\theta}$$ $$J\ddot{\theta} = L \left( -f_1+f_2 \right)$$

*

$$\frac{d}{dt}\left( \frac{\partial{\mathscr{L}}}{\partial{\dot{\phi}}} \right) - \frac{\partial{\mathscr{L}}}{\partial{\phi}} = 0$$ $$(j+ml^2)\ddot{\phi} - ml \left( \ddot{x}\cos{\phi} + (\ddot{z}+g)\sin{\phi} \right) = 0$$

State Space Representation

We have now obtained 4 coupled ODEs that needs to be uncoupled to obtain a SSR.

$$\begin{cases} \ddot{x} - \frac{ml}{M+m} \cos{\phi} \ddot{\phi} = - \frac{ml}{M+m} \sin{\phi} \dot{\phi}^2 - \frac{1}{M+m} \sin{\theta} (f_1 +f_2) \\ \ddot{z} - \frac{ml}{M+m} \sin{\phi} \ddot{\phi} = \frac{ml}{M+m} \cos{\phi} \dot{\phi}^2 -g + \frac{1}{M+m} \cos{\theta} (f_1 +f_2) \\ \ddot{\theta} = \frac{L}{J}(-f_1+f_2) \\ \ddot{\phi} -\frac{ml}{j+ml^2}\left( \ddot{x} \cos{\phi} + (\ddot{z} + g) \sin{\phi} \right) = 0 \end{cases}$$

The above can be matricially rewritten as a linear system: $\begin{pmatrix} 1 & 0 & 0 & a \\ 0 & 1 & 0 & b \\ 0 & 0 & 1 & 0 \\ c & d & 0 & 1 \end{pmatrix} \begin{pmatrix} \ddot{x}\\ \ddot{z} \\ \ddot{\theta} \\ \ddot{\phi} \end{pmatrix} = \begin{pmatrix} e \\ f \\ g \\ h \end{pmatrix}$

The system has full rank ( $det(A) = 1$ ).

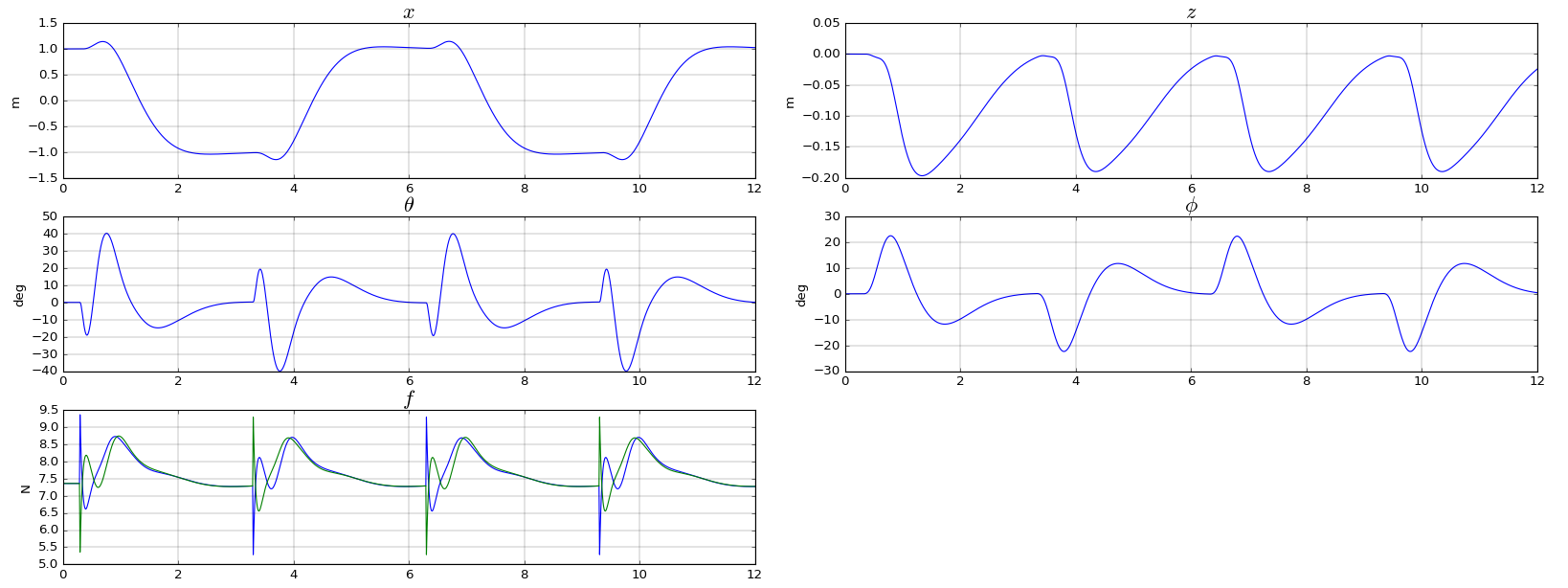
Simulation

The dynamic model for the pvtol pole is available in the file pvtol_pole.py. A openai gym compatible environment is avaible in the file pvtol_pole_env.py.

Fig3. - Simulation of the PVTOL pole under the authority of a linear regulator.

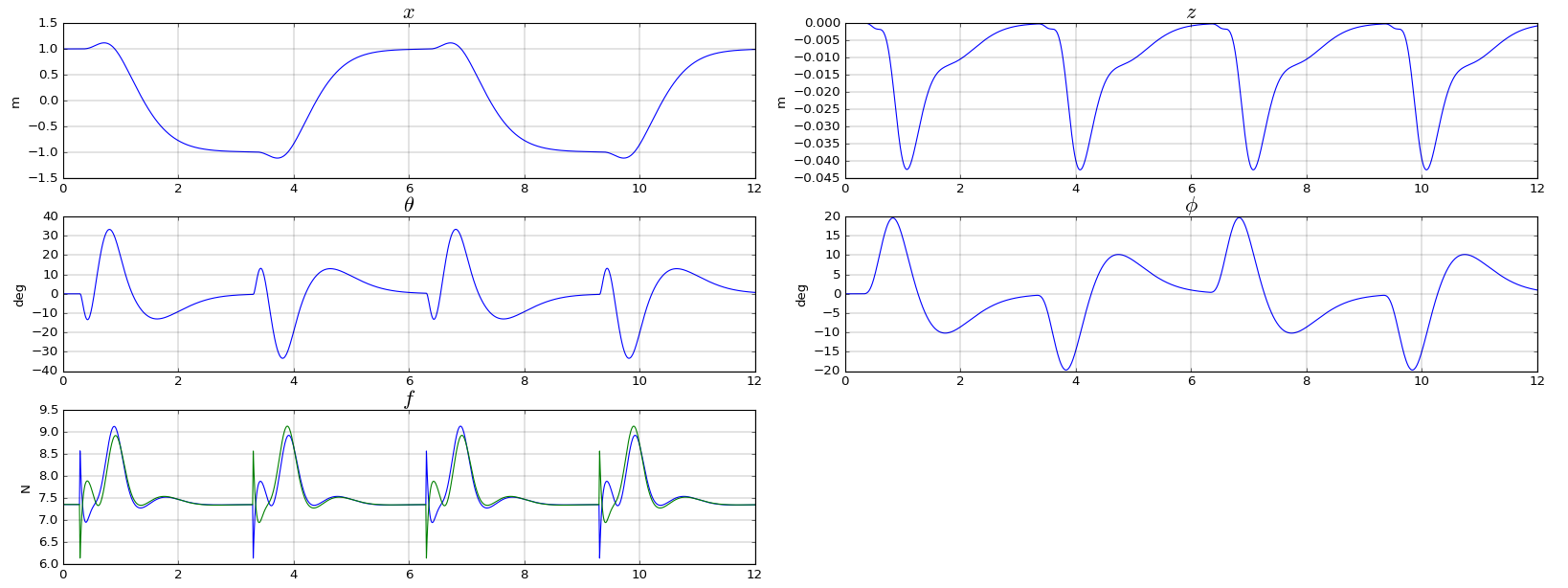
Figure (3) shows a simulation of the model under the authority of a linear regulator, obtained with this code.

Fig4. - Simulation of the PVTOL pole under the authority of a linear regulator.