$$\newcommand{\vect}[1]{\underline{#1}} % vector \newcommand{\mat}[1]{\mathbf{#1}} % matrices \newcommand{\est}[1]{\hat{#1}} % estimate \newcommand{\err}[1]{\tilde{#1}} % error \newcommand{\esterr}[1]{\tilde{#1}} % error \newcommand{\pd}[2]{\frac{\partial{#1}}{\partial{#2}}} % partial derivatives \newcommand{\transp}[1]{#1^{T}} % transpose \newcommand{\inv}[1]{#1^{-1}} % invert \newcommand{\norm}[1]{|{#1}|} % norm \newcommand{\esp}[1]{\mathbb{E}\left[{#1}\right]} % expectation \newcommand{\identity}[0]{\mathbb{I}} % identity \newcommand{\jac}[3]{\frac{\partial{#1}}{\partial{#2}}|_{#3}} % Jacobian$$

1: Derivation

Here we establish the expression of the heading needed by the drone to intercept a single target.

Figure 1. - Notations

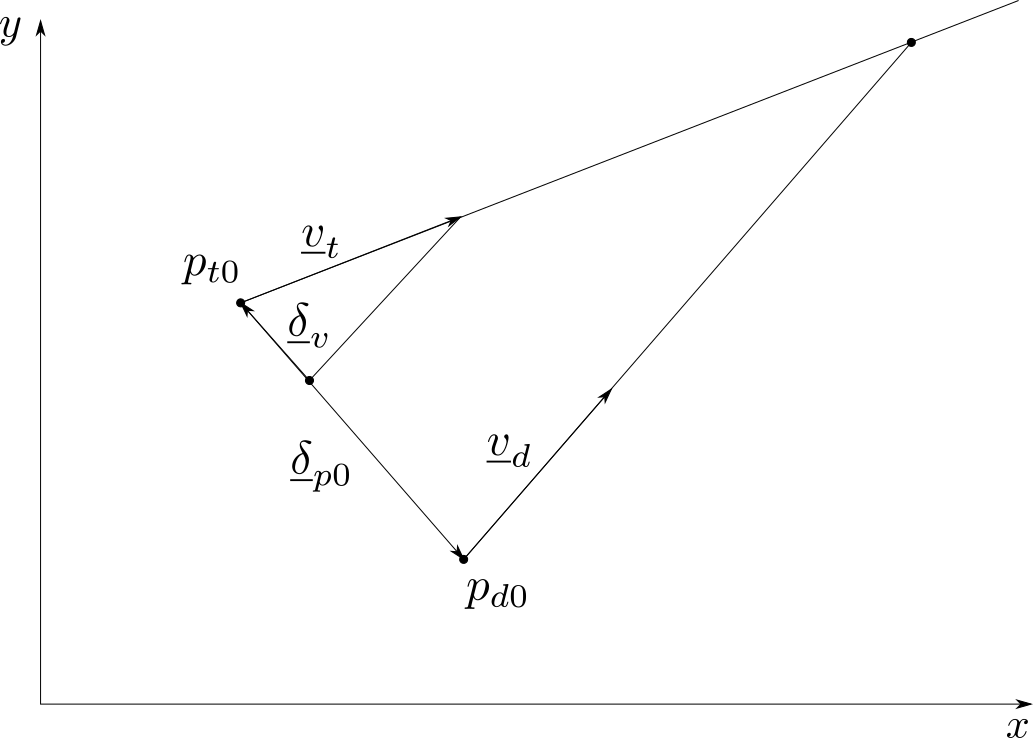
Using the notations presented in figure 1, the position of the drone and the target are given by:

\[\begin{equation} \vect{p}_d= \vect{p}_{d0} + \vect{v}_{d}.t \label{eq:pos_drone} \end{equation}\] \[\begin{equation} \vect{p}_t= \vect{p}_{t0} + \vect{v}_{t}.t \label{eq:pos_target} \end{equation}\]

At interception, using \eqref{eq:pos_drone} and \eqref{eq:pos_target}, we have:

\[\vect{p}_d == \vect{p}_t \iff \vect{p}_{d0} + \vect{v}_{d}.t = \vect{p}_{t0} + \vect{v}_{t}.t\]

Rearanging, we get

\[\begin{equation} t . \vect{\delta_v} = -\vect{\delta_{p0}} \label{eq:intercept_cond} \end{equation}\]

where \(\vect{\delta_v} = \vect{v}_{d}-\vect{v}_{t}\) and \(\vect{\delta_{p0}} = \vect{p}_{d0}-\vect{p}_{t0}\) are the differences between drone and target velocities and initial positions.

Condition \eqref{eq:intercept_cond} imposes

\[\begin{equation} \vect{\delta_v} \wedge \vect{\delta_{p0}} = 0 \label{eq:intercept_cond1} \end{equation}\]

Expressing \(\vect{\delta_v}=\begin{pmatrix}v_d \cos{\psi_d} -v_{tx}\\v_d \sin{\psi_d} -v_{ty}\end{pmatrix}\) and noting \(\vect{\delta_{p0}} = \begin{pmatrix}\delta_{p0x}\\\delta_{p0y}\end{pmatrix}\), \eqref{eq:intercept_cond1} can be rewritten as

\[(v_d \cos{\psi_d} -v_{tx})\delta_{p0y} - (v_d \sin{\psi_d} -v_{ty})\delta_{p0x} = 0\]

or

\[\begin{equation} a \cos{\psi_d} + b \sin{\psi_d} = c \label{eq:intercept_cond2} \end{equation}\]

with

\[\begin{equation} a=v_d \delta_{p0y} \qquad b=-v_d \delta_{p0x} \qquad c=v_{tx}\delta_{p0y} - v_{ty}\delta_{p0x} \end{equation}\]

Substituting variable \(\lambda = \tan{\frac{\psi}{2}}\) (inverted as \(\psi=2arctan{\lambda}\)), we get

\[\cos{\psi} = \frac{1-\lambda^2}{1+\lambda^2} \qquad \sin{\psi} = \frac{2\lambda}{1+\lambda^2}\]

and \eqref{eq:intercept_cond2} becomes a second order polynomial

\[(a+c) \lambda^2 -2b \lambda + (c-a) = 0\]

which can be solved for its roots \((\lambda_1, \lambda_2)\), leading to a pair of headings \((\psi_1, \psi_2)\)

Condition \eqref{eq:intercept_cond} can now be used once again to select the correct heading by enforcing

\[\begin{equation} \vect{\delta_v} . \vect{\delta_{p0}} < 0 \label{eq:intercept_cond3} \end{equation}\]

for \(t\) positiveness.

\(t\), the time of interception is then obtained from \eqref{eq:intercept_cond} as:

\[t = \frac{|\vect{\delta_{p0}}|}{|\vect{\delta_v}|}\]

Existence of a solution

As long as the forward velocity of the drone is strictly greater than the velocity of the target, a solution exists, by construction (TODO: show it, or just think about your chances of escaping when being chased by a faster guy…).