Dual pvtol, no load
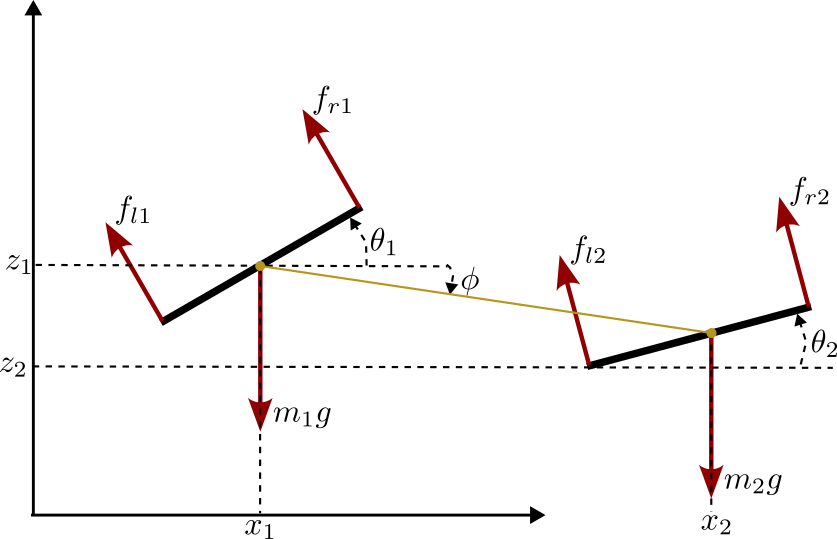
1: Model
- Generalized coordinates
- Kinematic
- Kinetic energy
Introducing our generalized coordinates leads to
\[T = \frac{1}{2} \left(m_1+m_2\right) (\dot{x}^2+\dot{z}^2) + \frac{1}{2} J_1 \dot{\theta}^2 + \frac{1}{2} m_2 l\dot{\phi} \left(l\dot{\phi} - 2(\dot{x}\sin\phi-\dot{z}\cos\phi\right)+ \frac{1}{2} J_2 \dot{\theta}_2^2\]- Potential energy
Introducing our generalized coordinates leads to
\[V = (m_1+m_2) g z + m_2 g l \sin{\phi}\]Lagrangian
\[\mathcal{L} = T - V\]- Partial derivatives
Lagrange equations
- \[\frac{d}{dt}\left( \frac{\partial{\mathcal{L}}}{\partial{\dot{x}}} \right) - \frac{\partial{\mathcal{L}}}{\partial{x}} = F_x\]
- \[\frac{d}{dt}\left( \frac{\partial{\mathcal{L}}}{\partial{\dot{z}}} \right) - \frac{\partial{\mathcal{L}}}{\partial{z}} = F_z\]
- \[\frac{d}{dt}\left( \frac{\partial{\mathcal{L}}}{\partial{\dot{\theta}}} \right) - \frac{\partial{\mathcal{L}}}{\partial{\theta}} = M_\theta\]
- \[\frac{d}{dt}\left( \frac{\partial{\mathcal{L}}}{\partial{\dot{\theta_2}}} \right) - \frac{\partial{\mathcal{L}}}{\partial{\theta_2}} = M_{\theta_2}\]
- \[\frac{d}{dt}\left( \frac{\partial{\mathcal{L}}}{\partial{\dot{\phi}}} \right) - \frac{\partial{\mathcal{L}}}{\partial{\phi}} = M_\phi\]
State Space Representation
Using \(X = \begin{pmatrix}x&z&\theta&\phi&\theta_2&\dot{x}&\dot{z}&\dot{\theta}&\dot{\phi}&\dot{\theta_2}\end{pmatrix}^T\) as state and \(U = \begin{pmatrix}f_l & f_r &f_{l2} & f_{r2} \end{pmatrix}^T\) as input, a state space representation can be obtained as:
\[\ddot{\phi} = \frac{m_1}{(m_1+m_2)l} (f_{l2}+f_{r2}) \cos(\phi-\theta_2) - \frac{m_2}{(m_1+m_2)l} (f_{l1}+f_{r1}) \cos(\phi-\theta_1) \\ \ddot{x} = -u_{t1}*\sin(\theta_1) - u_{t2} \sin(\theta_2) + \frac{l m_1}{m_1+m_2}\left(\ddot{\phi} \sin(\phi)+ \dot{\phi}^2\cos(\phi)\right) \\ \ddot{z} = u_{t1}\cos(\theta_1) + u_{t2}\cos(\theta_2) - g - \frac{l m_2}{m_1+m_2}\left(\ddot{\phi} \cos(\phi)-\dot{\phi}^2 \sin(\phi)\right) \\ \ddot{\theta} = (-f_{l1}+f_{r1})\frac{d_1}{J_1}\\ \ddot{\theta}_2 = (-f_{l2}+f_{r2})\frac{d_2}{J_2}\\\]2: Control
Master slave control
